『The Puzzling World of Polyhedral Dissections』という本に出ていた、「Geometrical Dissections」(幾何学的分割)というパズルがある。これは幾何学図形を分割したピースを使って、別の図形を作るものであるが、これでよく知られているのが、1902年にHenry Dudeneyが正方形を分割して、正三角形を作るという分割法を考案した。ネットで調べると、これ自身が数学的研究対象になっているようなので、理論的な事を知りたい方は調べてみられるとよい。ここではパズルとして、アクリル板を使ったピース作成について述べることとする。
図1 加工したピース最初に、分割についての説明をしておく。前述の本には、正方形の1辺を1としたときに、変換してできあがる正三角形の1辺が2／4√3(分子が2，分母は4乗根3)としか書かれておらず、分割法の詳細が不明であった。ネットで調べたところ、次のように作図する方法を見つけた。こちらは正三角形から分割する方法について書かれてる。
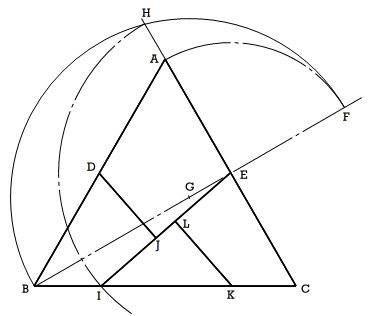図2 分割法の説明(1)正三角形ABCを作図する(作図法はおわかりかと思うのでパスする)。D、Eは辺の中点である。
(2)BEを結ぶ線分を引く。線分は延長しておく。AEを半径とする円を描き、線分BEの延長との交点をFとする。
(3)線分BFの中点をGとする。Gを中心にBGを半径とする円を描く。線分ACの延長との交点をHとする。
(4)Eを中心にEHを半径とする円を描く。BCとの交点をIとする。IとEを結ぶ。
(5)Dを通り、線分EIに垂直な線をひく。
(6)Iより線分AEの長さをとり、この点をKとする。Kを通り、EIに垂直な線分を引く。
以上の作図より、四角形ADIE、四角形DBIJ、四角形ELKC、三角形LIKの4つがピースである。
筆者は、正方形の一辺が100mmになるようにした場合のピースをパソコンの簡易CADで作成した。これを図3に示す。ただし、各部の寸法と角度は作図したものから求めているので、誤差がある。製作上は問題はあまりないと思う。
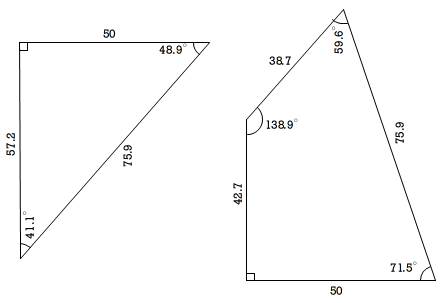図3 ピースの寸法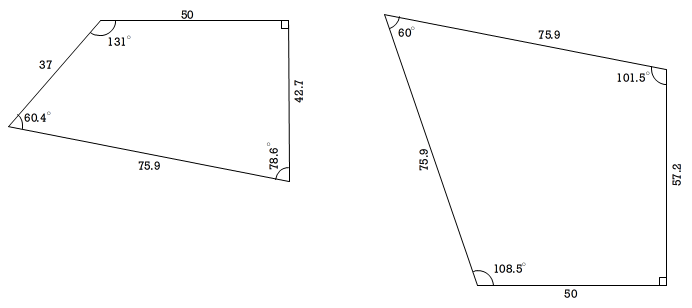
筆者は、これらのピースを印刷して2mm厚のアクリル板にはりつけて加工した。
図4 ピースの型紙をはりつけた図4をみれば、正方形の方の解答はわかる。正三角形については図1を参照のこと。これらを参考にピースがうまく収まるように調整されたい。
遊ぶときは、もちろんピースはバラバラの状態でわたすこと。ピースに1個所ずつ直角のところがあるので、正方形はわかりやすいと思われる。
【参考】
・『The Puzzling World of Polyhedral Dissections』Stewart T.Coffin, 1998Edition
・https://polyhedr.com/dudeny-dissection.html
<HOMEに戻る>