プロンプチュアリー(Promptuary) 2025.5.21
16世紀の数学者ネイピアが発明した「ネイピアの骨」という乗算具はよく知られているが、彼が「ネイピアの骨」を紹介した著書『Rabdologiae』にはこの他にも2つの計算具が紹介されている。今回は、そのうちの1つ「プロンプチュアリー(Promptuary)」を紹介したい。
図0 プロンプチュアリーが掲載されているRabdologiaeのページこれはネイピアの骨の拡張版とも言える計算補助具で、2種類のロッドを使用して乗算が簡単に行えるものである。ネイピアの骨では中間結果を書き留める必要があったが、プロンプチュアリーでは、桁上げさえ注意すれば、簡単に乗算結果を求めることができる。
図1 567×234の計算製作はネイピアの骨よりも少々骨が折れる(笑)。数字を表示する「窓」を作らなければいけないためである。だが、なかなか洗練されたものだといえる。製作は原図を簡易製図ソフト「花子」で描き、それをA4判のシール用紙に出力した。これを厚紙に貼り付け、ロッドとした。数字の書かれているロッドは厚さ2mmのボール紙に貼り付けた。窓のあるロッドには0.5mmのボール紙を使用した。厚さ2mmのボール紙を使ったのは、製本の表紙に使用した厚紙の切れ端が大量にあったのでこれを使用したためである。「何かの役に立つとよいが」と捨てずにとっておいたのが役に立った。改めて購入する人は、ケント紙などが使いやすいと思われる。
(1)数字ロッドの製作
数字ロッドは、ネイピアの骨で使われている「格子計算」という方法を使用したもので、1つのグループにはその数の九九が記されている。これが1つのロッドに5グループある。つまり5桁の乗算ができるということである。グループの数を増やせば、さらに多数桁の乗算が可能である。計算時にはこのロッドは縦長に配置される。
1つのグループの枠に記入する数字の規則を図2に示す。中央の対角線を境に、下側には1の位を、上側には10の位を記入する。
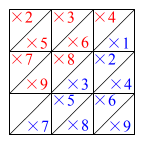図2 記入する数字の規則 
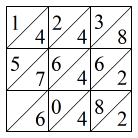図3 「8」の場合の記入例こうした正方形のグループを1～9について作成する。計算上は「0」も必要になるが、「0」の場合はすべてが0であるから、何も書かないロッドを用意すればよい。数字の記入位置を間違えないように作ることが必要である。こうした正方形を5つ縦に並べる。例として「8」のロッドを図4に示す。
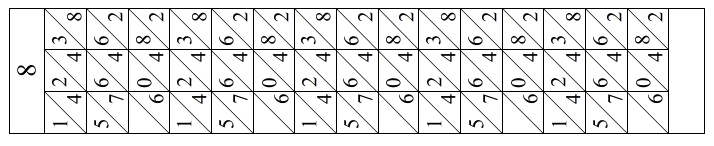
図4 「9」のロッド
0～9の数字ロッドは最後の項でPDFファイルがダウンロードできるようにしてある。印刷時に各自が用意した堅い紙の寸法に合わせて縮尺されたい。原図は横33mm×縦184mmである。作業としては厚紙を必要な寸法にカットし、印刷したシールをその大きさにカットして貼り付ける。私の場合は、厚紙が厚かったのでシールを貼り付けてからではカットしにくいのでこういう順番で行ったが、シールを厚紙全面に貼り付けてからカットしてもよい。
(2)窓ロッドの製作
窓ロッドは、数字ロッドに対し直角に置かれる。それぞれの数字ごとに図5のような窓をあけた正方形を5つ並べる。
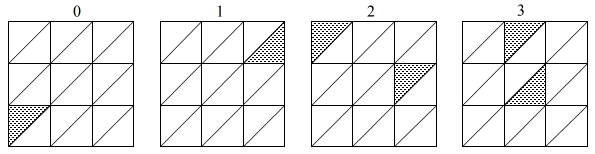
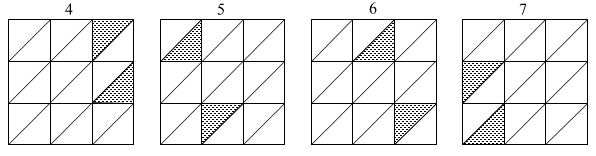
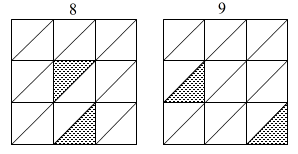図5 窓のパターン図「5」の窓ロッドの例を図6に示す。このロッドについても最後の項でPDFファイルがダウンロードできる。
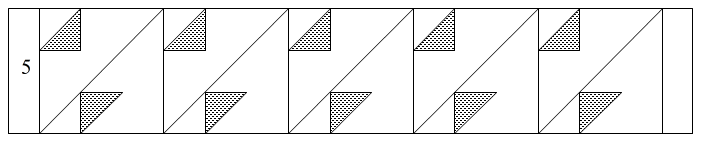
図6 「5」の窓ロッド
図5や6で網掛けになっている部分が窓になる。これも図をシール用紙にプリントアウトしてから、厚紙に貼り付け、窓をくりぬいてから、それぞれのロッドに切り離しす。切り離したあとで窓を開けるよりもこの順番の方がやりやすいと思われる。普通のカッターでも窓あけは可能だが、刃が細い「デザインナイフ」といわれるものがあけやすい。私はNTカッターのD-400というものを使用した。
(3)計算方法
例として 567×234 という乗算をやってみたい。567の数字ロッドを縦に左から右へと並べる。234は窓ロッドで横に上から下に並べる。これが図7である。
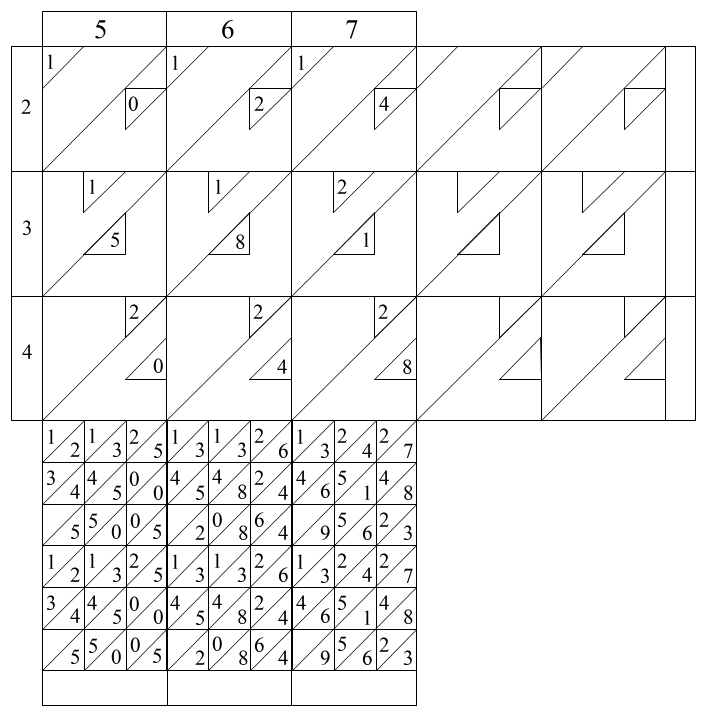
図7 567×234の乗算を行う並べ方
ここで窓ロッドの対角線がそれぞれの桁の区切りとなる線である。この斜線の範囲に出てくる数字を加算していく。繰り上がりがあるときは1つ上の桁に加算する。図8にその様子を示す。
図8 計算の様子
・A： 1 しかないので、これが最上位桁となる。
・B： 1、0、1 とあるので、加算して2となる。
・C： 1、2、1、5、2 となるので、加算して11となる。10の位はBに桁上げする(よってBは3となる)。
・D： 4、2、8、2、0 となるので、加算して16となる。10の位はCに桁上げする(よってCは2となる)。
・E： 1、2、4 となるので、加算して7となる。
・F： 8 しかないの、これが最下位桁となる。
結果として、132678 が解答である。
電卓で簡単に計算ができる時代に、こうした計算具は無用の長物かもしてない。しかも日本の子どもたちは九九を暗記しているのでなおさらである。きっとなぜこんな面倒なことをしたのかが理解できないだろう。だが、昔は九九の表を暗記することなどはなかったので(現在でもそういう国はある)、乗算は九九の表を片手に行わなければならなかった。そういう事情がわかると、なぜこうした計算補助具が求められたのかが少しは理解できるのではないだろうか。
■プロンプチュアリーの数字ロッドと窓ロッドのダウンロードは こちら。
最後に、私は余りの厚紙をボンドで接着して箱を作り、その中にプロンプチュアリーのロッドを収納した。外側に、100円ショップで売っていた包装紙の余りを貼り付けると少しは格好がよくなった。
図9 箱に収めた【参考】
"Promptuary https://en.wikipedia.org/wiki/Promptuary
【図の出典】
図0 ：https://archive.org/details/rabdologiae00napi/page/102/mode/2up?view=theater
<HOMEに戻る>